O que eles tem em comum?
Módulo Mobilidade
Disciplina de Robôs Móveis Autônomos
Engenharia de Instrumentação Automação e Robótica
Profa. Dra. Elvira Rafikova
elvira.russa@gmail.com
Conteúdo do módulo
- Locomoção robótica
- Robôs com pernas
- Robôs com rodas
- Modelagem cinemática e dinâmica de robôs
O que tem de diferente?
Terrestre:
Robô terrestre com pernas ou rodas . Há também locomoção com esteiras e conjuntos híbrido.
Aéreo:
Drones, aviões autônomos com diversos motores, principalmente elétricos (brushless) e hélices como sistemas de propulsão
Aquático:
Grande variedade: submarinos autônomos, AUVs , veículos de superfície, peixes artificiais biomiméticos, ROVs , Gliders. Propulsão por motores elétricos, deslocamento de volume de água, velas, ondas, movimento de caudas e nadadeiras.
LocomoçÃo
Determinada pelo meio de atuação do robô móvel já que locomoção é , de fato, a interação física entre o robô e seu meio.
Locomoção Aquática
Locomoção em meio aquático é muito diversificada já que a diversidade de robôs aquáticos é muito grande. Mas um caso é muito interessante: Underwater Glider
robôs aquáticos
- UAV – Underwater Autonomous Vehicle , Underwater Unmanned Vehicle ( todos os veículos submersíveis)
- Submarinos autônomos
- Gliders
- ROV – Remotely Operated Vehicle : cordão umbilical
- Catamarãs : de superfície
- Barcos autônomos
- Hovercraft: veículo aerosuportado
Locomoção Terrestre
robôs com Pernas
Hoppers, Bípedes, Humanóides, Quadrúpedes, Hexápodes
Locomoção mais apropriada para terrenos acidentados e irregulares. Desafios de coordenação de pernas. Quanto mais articuladas mais atuadores , mais pesado o conjunto. Muitos imitam a natureza- biomiméticos.
Robôs com rodas
Rodas são mais apropriadas para terrenos planos, estruturados , onde essa locomoção é mais eficiente. Nesse terreno tem-se baixo custo energético para atuação e velocidades bem superiores a pernas.
Veículos podem ser de 1 até 4 rodas em geral. Diferentes tipos de rodas e diferentes arranjos cinemáticos determinam a mobilidade e manobrabilidade do veículo.
híbridos
Esteiras ( caterpillars) , como as que se usava em tanques de guerra, são conjuntos de rodas unidos por uma correia e são muito populares em robótica pois permitem transposição de terrenos acidentados ao mesmo tempo sendo manobráveis como um arranjo de duas rodas diferenciais .
Outros: arranjos com pernas e rodas , como na figura, unem o melhor dos dois mundos
Robôs com Pernas
hoppers
Uma perna em equilíbrio dinâmico que se move saltando e direcionando o ângulo do quadril. Mais econômico pois cada perna significa mais peso e coordenação mais difícil.
bípedes
Duas pernas , em geral são humanóides ou biomiméticos.
quadrúpedes
Quadrúpedes podem imitar a locomoção de animais quadrúpedes que usam dois tipos de marcha com equilíbrio estático ou dinâmico.
hexápodes
Seis pernas, imitando insetos, locomoção mais vantajosa com movimento de 3 pernas por vez simultaneamente. Assim a marcha sempre é dinamicamente estável , com 3 apoios, e a coordenação tem poucos eventos .
Tipos de rodas
Rodas Padrão
Rodas comuns encontradas em carros. Roda em torno do eixo central. Não desliza lateralmente
Direcionáveis: possui mais um eixo em torno do qual há movimento para direcionamento
roda castor
Roda com dois eixos de movimento , caracteristicamente distantes de d , também chamado de eixo de caster.
Rodas de carrinho de supermercado e cadeiras de escritório.
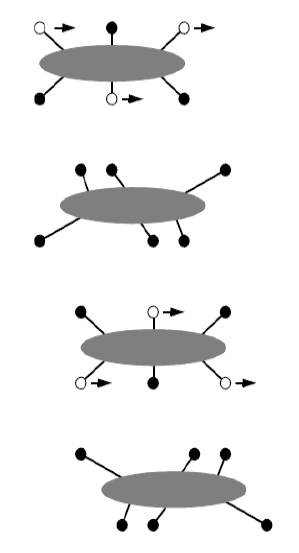
rodas suécas
Rodas cuja banda é coberta por pequenos rodízios com giro livre. Dependendo do angulo entre o eixo desses rodízios e o vetor velocidade da roda temos :
SUECA 45
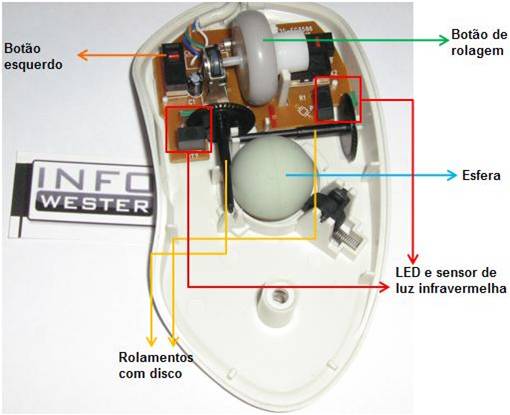
roda esférica
Usada como rodízio livre, já que é difícil de atuar e quantificar o movimento.
FIGURA DO MOUSE de bolinha
SUECA 90
arranjos de rodas
acionamento diferencial - Differential steering
O arranjo mais popular em robótica no qual as duas rodas comuns , fixas, paralelas são acionadas independentemente. A diferença causa a mudança de orientação
Triciclo e quadriciclo Ackermann
Dois conjuntos de rodas , frontal e traseiro que podem ou não ser atuados e /ou direcionáveis. Chassis Ackermann tem a particularidade de direcionar as rodas de forma desigual, formando um ângulo entre as rodas direcionáveis que estabiliza o veículo em curvas e evita forças desnecessárias aos eixos de fixação.
mecanum
Arranjo com 4 rodas suecas 45 dispostas em pares e com oposição angular. Dessa forma o arranjo se torna omnidirecional
Arranjo omnidirecional significa que o veículo consegue se locomover o melhor, consegue setar o vetor velocidade para qualquer direção em qualquer instante do tempo.
Omnidirecional 3 rodas suecas 90
Arranjo que pressupõe corpo redondo pois a sua disposição das rodas é de simetria radial.
Arranjo Synchro drive
3 rodas acionadas por 2 atuadores, com movimento pseudo-omnidirecional, um para acionar as rodas, outro para direcionar ( usando correias e polias para transmissão do movimento)
Modelagem Cinemática dos veículos
Considerações sobre posição e velocidades para se chegar a um modelo de deslocamento do veículo. Cada propulsor ou roda contribui para o deslocamento do veículo. A modelagem cinemática descreve exatamente isso.
Definições
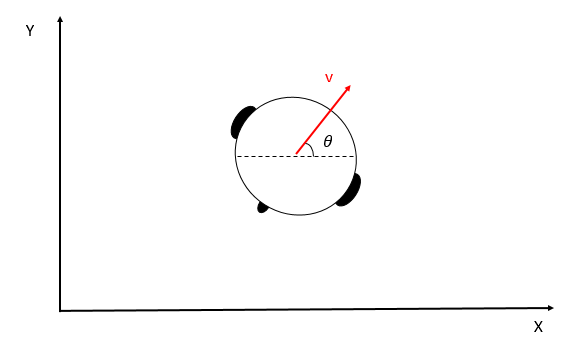
Velocidade linear:
Velocidade angular do robô:
Velocidade de rotação das rodas ( angular ) :
Ângulo de orientação do robô:
Raio da roda:
Raio do corpo do robô:
v$$\omega$$
$$\dot{\varphi}$$$$\vartheta$$
r
L
Relação entre velocidades angular e linear :$$v=\omega r$$
Equações de movimento são funções características da geometria e das velocidades do robô: $$\dot{\xi}= \left[ \dot{x} \hspace{4 pt} \dot{y} \hspace{4 pt} \dot{\vartheta} \right]^T= f ( l, r, \vartheta ,\varphi_1 , \varphi_2 )$$
Robô de acionamento diferencial
Duas rodas do tipo padrão fixas, que são acionadas independentemente. O centro do corpo está exatamente no ponto central entre as rodas.
1. Computar quanto cada roda contribui ao movimento do referencial do robô
2. Computar as velocidades no referencial do robô
3. Transformar para referencial global
Cada roda: $$\frac{\dot{\varphi_d} r}{2}$$
No referencial do robô :
$$v_x=\dot{x_R}= \frac{\dot{\varphi_d} r}{2}+ \frac{\dot{\varphi_e} r}{2}$$$$v_y=\dot{y_R}=0$$$$\omega=\dot{\vartheta}=\frac{\dot{\varphi_d} r}{2l}- \frac{\dot{\varphi_e} r}{2l}$$
Transformação para global:
$$\begin{eqnarray} \left[ \begin{matrix} \dot{x}\\ \dot{y}\\ \dot{\vartheta} \end{matrix} \right]_G = \left[ \begin{matrix} \cos{\vartheta} & -\sin{\vartheta} & 0\\ \sin{\vartheta} & \cos{\vartheta} & 0\\ 0 & 0 & 1\\ \end{matrix}\right] \left[ \begin{matrix} \dot{x}\\ \dot{y}\\ \dot{\vartheta}\\ \end{matrix}\right]_R \end{eqnarray}$$
Resultando no Modelo de Deslocamento :
$$\begin{eqnarray} \dot{x}_G= \cos{\vartheta} \left[ \frac{\dot{\varphi_d} r}{2}+ \frac{\dot{\varphi_e} r}{2}\right]=v \cos{\vartheta} \\ \dot{y}_G= \sin{\vartheta} \left[ \frac{\dot{\varphi_d} r}{2}+ \frac{\dot{\varphi_e} r}{2} \right]= v \sin{\vartheta}\\ \dot{\vartheta}_G = \frac{\dot{\varphi_d} r}{2l}- \frac{\dot{\varphi_e} r}{2l}=\omega \end{eqnarray}$$
Cinemática Triciclo
Roda frontal direcionável ( neste caso também atuada) . As rodas traseiras são de rotação livre. O frame do robô é colocado entre as rodas traseiras.
Roda Direcionável :
$$V_s=\dot\varphi_s r cos \alpha=\dot x_R$$
No triciclo o ângulo $$\alpha$$ varia . A componente seno está orientada com a velocidade linear do robô em x (do robô). Já a componente seno se alinha não com o deslizamento lateral ( em y do robô ) , mas como velocidade tangencial à curva quando há rotação . Portanto influencia na velocidade angular do robô :
$$V_{sy}=\dot\varphi_s r sin \alpha$$
$$\omega=\dot \vartheta_ R=\frac{\dot{\varphi_s} r sin \alpha}{d}$$ A velocidade linear do robô na sua lateral ( y do robô ) é nula : $$\dot y_R=0$$
Em resumo : $$\begin{eqnarray} \dot x_R=\dot\varphi_s r cos \alpha \\ \dot y_R=0 \\ \dot\vartheta_R= \frac{\dot{\varphi_s} r sin \alpha}{d} \end{eqnarray}$$
Aplicando a transformação para coordenadas globais:
$$\begin{eqnarray} \left[ \begin{matrix} \dot{x}\\ \dot{y}\\ \dot{\vartheta} \end{matrix} \right]_G = \left[ \begin{matrix} \cos{\vartheta} & -\sin{\vartheta} & 0\\ \sin{\vartheta} & \cos{\vartheta} & 0\\ 0 & 0 & 1\\ \end{matrix}\right] \left[ \begin{matrix} \dot{x}\\ \dot{y}\\ \dot{\vartheta}\\ \end{matrix}\right]_R \end{eqnarray}$$
Aprofunde o conhecimento:
Leia os slides para aprofundar o conhecimento teórico e acesse os links indicados :
Avaliação do Módulo
Responda o roteiro:
VOLTAR para Página de Disciplina de Robôs Móveis Autônomos
Fontes de Imagens :
https://secoora.org/underwater-gliders-chasing-hurricane-florence/
https://earthzine.org/going-deep-to-go-far-how-dive-depth-impacts-seaglider-range/
https://www.theverge.com/2018/6/28/17514134/honda-asimo-humanoid-robot-retire
https://hackaday.com/2017/05/24/hackaday-prize-entry-underwater-glider-offers-low-power-exploration/
https://www.core77.com/posts/47205/Wheels-That-Permit-360-Degree-Movement—Without-Turning